Lineaire regressie is een krachtig gereedschap
Mits goed gebruikt, is lineaire regressie een krachtig stuk gereedschap om gegevens te onderzoeken. Daar staat echter tegenover dat je het evengoed kan gebruiken voor manipulatie van uitkomsten. Alles staat of valt met het kennen van het proces. En vooral met het kennen van de randvoorwaarden waarbinnen de statistische techniek gebruikt mag worden. Hieronder behandelen we het correcte gebruik van de lineaire regressie-techniek en laten daarmee en passant de aanpak van het misbruik zien binnen de kaders van predictive analytics.
De training R & data mining 
Tijdens deze training maak je in 3 dagen intensief kennis met het vakgebied Predictive Analytics, data mining & text mining. Ook de thema's big data, privacy en ethiek komen aan bod, maar je leert vooral programmeren in R & WEKA. De docent licht de verschillende soorten algoritmes toe. Je gaat met R oefenen en gebruikt technieken als lineaire regressie en logistische regressie.
Lineaire regressie en het kleinstekwadratenprincipe
Met lineaire regressie kan je een verband aantonen tussen twee of meer variabelen, bijvoorbeeld de buitentemperatuur en het aantal verkochte schaatsen, of iemands leeftijd en het aantal speelfilms dat iemand kijkt. De metingen van deze variabelen zet je uit in een assenstelsel en vervolgens bereken je een rechte lijn, de lineair. Dat kun je bijvoorbeeld doen op basis van het kleinstekwadratenprincipe.
Je komt dan op een lijn waarbij het totaal van de gekwadrateerde afwijkingen vanaf de lijn, verticaal gemeten, het kleinst is. Er zijn natuurlijk ook andere methoden om dit te doen. Wanneer er sprake is van een stijgende of dalende lijn, heb je een (eenvoudig) voorspellend model. Je hebt te maken met enkelvoudige lineaire regressie wanneer er sprake is van één afhankelijke variabele (de schaatsen) is en één onafhankelijke variabele (de temperatuur).
Meervoudige lineaire regressie
Bij meervoudige lineaire regressie heb je te maken met meerdere onafhankelijke variabelen, bijvoorbeeld temperatuur en het land. Onafhankelijke variabelen noem je verklarende of voorspellende variabelen. De term lineaire regressie is ontstaan toen de wetenschapper Francis Galton, een halfneef van Charles Darwin, een patroon ontdekte in de nakomelingen van lange mensen.
Francis Galton
Uit onderzoek dat Galton deed in het midden van de negentiende eeuw bleek dat de nakomelingen van lange mensen steeds korter worden totdat zij op de gemiddelde lengte uitkomen. Hij noemde dit effect lineaire regressie omdat de afname in lengte, de regressie, min of meer lineair plaatsvond. Bij het uitwerken van zijn metingen gebruikte Galton een gedegen statistische omschrijving. Latere onderzoekers namen de benaming en de statistiek over, maar pasten deze toe op andere metingen, ook metingen waarbij er sprake was van een toename.
Logistische regressie
In een flink aantal gevallen kun of wil je lineaire regressie niet toepassen, bijvoorbeeld omdat de afhankelijke variabele een vaste uitkomst kent (ja/ nee), of een onder- en een bovengrens. Dit is bijvoorbeeld het geval wanneer je lineaire regressie gaat toepassen op een dataset met het aantal studieminuten per leerling en de slagingskans voor het tentamen van dat vak. Die ligt tussen de 0% en de 100%. Je kunt immers niet 101% of -10% kans hebben om te slagen.
Daarnaast is er niet altijd sprake van een doorlopend lineair verband en wil je juist meer kennis opdoen. In een bepaalde range van de onafhankelijke variabele aantal studieminuten, bijvoorbeeld tussen de 0 en 25 minuten, is de slagingskans erg laag (maximaal 10%), maar tussen de 25 en 50 studieminuten zie je de kans sterk toenemen tot 40%. En bij meer dan 60 studieminuten neemt de kans weer sterk af.
Kortom: de lineaire regressie overschat de slagingskans bij weinig studieminuten en onderschat die bij veel studieminuten. Dit zijn voorbeelden waarbij je een logaritmische curve (gemaakt met logistische regressie) wil zien die veel nauwkeuriger voorspelt.
Het probleem dat lineaire regressie laat zien
De werking van lineaire regressie is uitstekend te illustreren via een eenvoudig natuurkunde-experiment waarin de uitrekking van een veer wordt gemeten als functie van de zwaartekracht Fz op een blokje dat aan de veer hangt. De grootte van de zwaartekracht Fz hangt direct af van de massa m van het blokje dat aan de veer hangt volgens Fz= mg, waarin g = 9,81ms2 de zwaartekrachtversnelling is. Vervolgens wordt de uitrekking x van de veer gemeten voor verschillende waarden van de zwaartekracht Fz. Bedenk dat steeds de massa m van het blokje wordt gekozen en daarmee de grootte van de zwaartekracht Fz wordt bepaald.
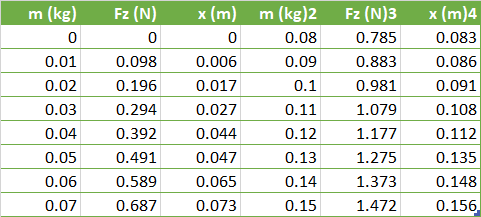
Tabel 1: Meting van de uitrekking x van de veer als gevolg van de zwaartekracht Fz op een blokje met massa m.
Uit de getallen in bovenstaande tabel blijkt dat de uitrekking x toeneemt als de zwaartekracht Fz toeneemt. Maar het is niet direct duidelijk of er sprake is van een zekere wetmatigheid. Door de gegevens in een diagram te zetten, begint zich een wetmatigheid af te tekenen. Het lijkt erop dat er mogelijk een lineair verband tussen de kracht Fz en de uitrekking x bestaat.
Lineair verband?
Stel, er bestaat inderdaad een lineair verband tussen de grootte van de zwaartekracht Fz en de uitrekking x van de veer, dus:
x=C1 Fz+ C2
waarin C1 en C2 constante getallen zijn. In dat geval zijn er twee vragen die je moet beantwoorden:
- Hoe kan je de meest geschikte rechte lijn door de meetpunten vinden? Anders gezegd, is het mogelijk om de grootte van C1 en C2 te bepalen?
- Hoe betrouwbaar is de gevonden vergelijking? Anders gezegd, hoe nauwkeurig kun je x berekenen vanuit Fz en omgekeerd?
De oplossing die lineaire regressie heet
Neem aan dat de verschillende meetpunten op een rechte lijn liggen. Deze rechte lijn beschrijf je met de vergelijking zodat met het bepalen van de constante getallen C1 en C2 het verband tussen de zwaartekracht Fz en de uitrekking x vastligt. In het precomputertijdperk werd de betreffende lijn met een liniaal zo goed mogelijk midden tussen de meetpunten door gematst.
Het was dan de truc om de gemiddelde afstand tussen de verschillende meetpunten en de getrokken lijn zo klein mogelijk te houden. De reden voor dit handmatig bepalen van de lijn en daarmee ook van de constante getallen C1 en C2 lag in de hoeveelheid rekenwerk die nodig is voor het rekenkundig bepalen. Hoewel het rekenwerk op zich niet moeilijk is, is het dermate tijdrovend dat een ervaren rekenaar voor één diagram ongeveer een hele dag nodig had.
Bepaal de minimale afstand tussen de meetpunten
Het principe van lineaire regressie is dat er een lijn bepaald wordt die een minimale afstand heeft tot de verschillende meetpunten. Veel pakketten voor het verwerken van gegevens, zoals een spreadsheet, kennen deze procedure. Het bepalen van deze lijn is dus een puur wiskundige (rekenkundige) procedure en kan je in principe op elke verzameling van meetgegevens uitvoeren.
Wordt het resultaat van de lineaire regressie toegevoegd aan het oorspronkelijke diagram, dan is het verband tussen de zwaartekracht Fz en de uitrekking x direct duidelijk. Hoe mooi een dergelijk diagram er ook mag uitzien en hoe goed het visueel ook mag kloppen, de vraag naar de kwaliteit van de benadering blijft. In de praktijk wordt dit opgelost door de correlatiecoëfficiënt r te bepalen.
Deze coëfficiënt geeft aan hoe goed de verschillende meetpunten op de berekende rechte lijn liggen waarbij r = 1 is voor de perfecte stijgende lijn en r = -1 voor de perfecte dalende lijn. Als r = 0 dan bestaat er geen verband tussen de meetpunten. Ook het berekenen van de correlatiecoëfficiënt is een bekende procedure voor het verwerken van gegevens.
Wat zijn de beperkingen?
Het bepalen van een lijn door een verzameling meetpunten is een puur wiskundige (rekenkundige) procedure. Je kan het in principe op elke verzameling van meetgegevens toepassen. Dit is aan de ene kant het sterke punt van deze procedure, maar aan de andere kant ook de achilleshiel. Zo moeten de gegevens aan bepaalde voorwaarden voldoen:
- Voorwaarde 1: De onafhankelijke grootheid kent (vrijwel) geen spreiding. Met andere woorden, van deze grootheid is de waarde exact bekend.
- Voorwaarde 2: De afhankelijke grootheid is een lineaire combinatie van de onafhankelijke grootheid. Dit betekent dat het verband beschreven kan worden met een polynoom.
- Voorwaarde 3: De variantie r in de afhankelijke grootheid is onafhankelijk van de grootte van de onafhankelijke grootheid.
Door aanpassingen in de rekenmethode is het mogelijk om een spreiding in de onafhankelijke grootheid (voorwaarde 1) op te nemen in de berekening. Dit geldt niet voor de andere voorwaarden.
De consequenties
Mocht aan één van deze voorwaarden niet voldaan worden, dan betekent dit:
- Situatie 1: Lineaire regressie is als techniek niet toepasbaar op de gebruikte verzameling gegevens.
- Situatie 2: Gebruik van lineaire regressie geeft geen betrouwbare uitkomsten.
- Situatie 3: Het probleem waarop lineaire regressie wordt toegepast is niet goed beschreven.
Welke van de drie genoemde situaties geldt, hangt af van (een analyse van) het probleem. Zelfs als de gegevens duidelijk geen lineair verband kennen, dan nog kan je met lineaire regressie een lijn berekenen. Heel illustratief in dit opzicht is Anscombe’s kwartet, ontwikkeld in 1973 door de Engelse statisticus Frank Anscombe. Dit kwartet bestaat uit vier verschillende verzamelingen meetpunten die na lineaire regressie eindigen met exact dezelfde lijn: (a) normaal (b) krom (c) piek (d) cluster.
Vier identieke verzamelingen
Niet alleen geeft de lineaire regressie dezelfde lijnen in de diagrammen. Ook de overige kengetallen van de vier verzamelingen zijn identiek. Wie alleen naar de getallen kijkt, ziet geen verschil tussen de vier diagrammen en zal ze als gelijkwaardig beschouwen. Nadere beschouwing van de spreidingsdiagrammen laat al snel zien dat de berekende lijn in zeker twee van de vier gevallen geen betekenis heeft.
- Gemiddelde van de x-waarden: 9
- Variantie van de x-waarden: 11
- Gemiddelde van de y-waarden: 7,50
- Variantie van de y-waarden: 4,122
- Correlatiecoëfficiënt: 0,816
- Lijn volgens lineaire regressie: y = 3,00 + 0,500x
Tabel 2: Kentallen van de diagrammen uit Ascombe’s kwartet.
Het verkorten van de assen
Ook het verkorten van de assen in een diagram of het werken met slechts een deel van de gegevens kan de suggestie wekken dat gegevens zich eenvoudig laten “lineariseren”, terwijl feitelijk het tegendeel waar is. Dit geldt in het bijzonder wanneer een deel van de beschikbare gegevens gebruikt wordt om een zeker verband af te leiden, waarbij dat afgeleide verband gebruikt wordt om de overige (of incomplete) gegevens te categoriseren.
Door te spelen met de schaal van de grafiek en de gepresenteerde waarden kan een bepaald verband gesuggereerd worden, terwijl de gegevens feitelijk anders spreken. Dit probleem kan zich voordoen bij technieken die gebruikmaken van bepaalde vormen van regressie zoals naaste buur. Vooral bij het toepassen van lineaire regressie om verbanden te zoeken tussen verschillende soorten gegevens wordt gesjoemeld met als enig doel het presenteren van een ‘gewenst’ antwoord.
Meer weten over regressie-technieken?
De specialisten van Passionned Group kennen als geen ander de (on)mogelijkheden van lineaire regressie en andere voorspellende algoritmes. Maak vrijblijvend een afspraak met een van onze data mining experts en laat je verrassen wat artificial intelligence voor jouw organisatie in petto heeft.
Over Passionned Group
De specialisten in statistiek en data mining van de Passionned Group helpen je graag verder met lineaire regressie technieken. Met als doel om jouw processen te verbeteren en innovaties door te voeren met business analytics. Om het jaar reiken we de Dutch BI & Data Science Award uit aan de Slimste organisatie van Nederland. 
